[超譯]ThinkDSP 第十章

第十章 線性非時變系統 | LTI systems

這章展示訊號與系統的理論，用音樂當範例。會解釋卷積理論的一個重要應用，線性、非時變系統(稍候會定義)的特徵化。
此章的程式碼在 chap10.ipynb，請參閱(0.2節)，也可以在後方連結參閱 http://tinyurl.com/thinkdsp10 。

10.1 訊號與系統

在訊號處理的領域裡，「系統 system」這名詞是個抽象的名詞，任何能輸入一個訊號之後產生另一個訊號的東西就叫系統。
例如一個電子放大器，它是將一電子訊號當輸入，然後產生一個(大聲一點)的訊號當輸出。
再一個例子，當你在聽音樂演奏時，你可以把那房間當成一個系統，演奏位置的聲音，經過房間的效應，傳到你耳朵聽到的聲音，兩者已有些許不同。
一個線性、非時變系統(註)，它具備兩個性質：

1. 線性(Linearity)：如果你同時給兩個輸入，它的和就是其輸出。以數學話來說，如果給個輸入 $x_1$ 會產生輸出 $y_1$，給另一個輸入 $x_2$ 會產生輸出 $y_2$。若給一個輸入 $a x_1 + b x_2$ 會產生輸出 $a y_1 + b y_2$。$a$ 與 $b$ 是純量。
2. 非時變(Time invariance)：系統的影響不會隨時間變化，或說不會依系統的狀態有變化。所以，如果輸入 $x_1$ 與 $x_2$ 只有時間上的差異，其他完全相同，則其對應的輸出 $y_1$ 與 $y_2$ 也只有時間上的差異，其他完全相同。

許多物理系統或多或少都有這些性質。

• 只有包含電阻、電容、電感的電路，是 LTI (線性非時變)系統。其中元件需是理想模型的狀況下。
• 機械系統裡有彈簧、質量、阻尼器也是 LTI 系統。其中彈簧是線性(力量與位移成正比)、阻尼器也是線性(力量與速度成正比)。
• 再來，本書中的許多應用如聲音的傳播(包含空氣、水、固體)，也是 LTI 系統。

LTI 系統可以用線性微分方程式表示，其解為複數正弦，請參見： http://en.wikipedia.org/wiki/Linear_differential_equation
因此，有個演算法可計算 LTI 系統對一個輸入的影響：

1. 將訊號表示為複數正弦成份的和。
2. 對每個輸入成分，計算對應的輸出成份。
3. 把每個輸出成份加總。

現在，我希望這個演算法你聽來熟悉，相同的演算法，在 8.6節用在卷積，在 9.3節用在微分。這個的流程叫「頻譜分解 spectral decomposition」因為我們「分解」輸入訊號成為它的光譜成份。
為了要將這個流程用在 LTI 系統，我們必須特徵化這個系統，藉由找到輸入訊號中每個成份的影響。對機械系統，一個簡單有效的的方法就是，踢它，然後記下其輸出。
技術上來說，「踢」就叫做「脈衝 impulse」，輸出叫「脈衝響應 impulse response」。你也許好奇，一個單一脈衝如何完整特徵化系統。答案是計算脈衝的 DFT。這裡有個 wave array 其中在 $t=0$ 有個脈衝：

    impulse = np.zeros(8)
    impulse[0] = 1
    impulse_spectrum = np.fft.fft(impulse)

它的 wave array 的內容：

[ 1.  0.  0.  0.  0.  0.  0.  0.]

然後這是它的頻譜：

[ 1.+0.j  1.+0.j  1.+0.j  1.+0.j  1.+0.j  1.+0.j  1.+0.j  1.+0.j]

這個頻譜全是一，也就是這個脈衝是由各頻率全相同振幅的成份組合而成。這個頻譜不要跟白噪音搞混，白噪音為各頻率相同平均功率，但在平均附近變動。
當你測試一個系統，輸入一個脈衝，你是在測試此系統全頻率的響應。你可以同時測試它們是因為系統是線性的，所以同時測試不會互相影響。

10.2 window 與濾波器 | Windows and filters

要顯示特徵化系統怎麼成功的，我用個小例子開始：一個 2-元素 的移動平均。我們可以想像這個系統的操作是取一個訊號為輸入，產生一個稍平滑的訊號為輸出。
在這個範例中，我們已知 window，所以我們可以計算對應的濾波器。但這種情況不多見。下一節我們會討論不知道 window 或濾波器的例子。

---

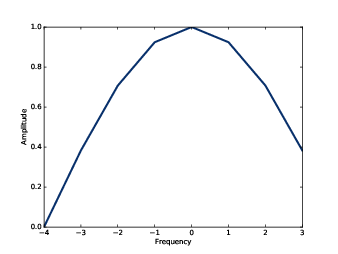
圖10.1：2-元素 移動平均的 DFT

---

底下是計算 2-元素 移動平均的 window 的過程(參見 8.1節)：

    window_array = np.array([0.5, 0.5, 0, 0, 0, 0, 0, 0,])
    window = thinkdsp.Wave(window_array, framerate=8)

我們可以計算 window 的 DFT 來得到對應的濾波器：

    filtr = window.make_spectrum(full=True)

譯註：因為原文的變數就叫 filtr，而且後來的程式碼也用同樣的字，就不去修正了。
結果顯示於圖10.1，對應移動平均的濾波器是低通濾波器，它的形狀接近高斯曲線。
現在來想像我們不知道 window 或是對應的濾波器，我們可以輸入一個脈衝(impulse)然後量測其脈衝響應。
在這個例子裡，我們可以把脈衝的頻譜乘上濾波器得到脈衝響應，然後從頻譜轉換成波：

    product = impulse_spectrum * filtr
    filtered = product.make_wave()

因為 impulse_spectrum 全是一，它的乘法結果也就等於濾波器，所以濾完的波也就等於 window。
這例子說明兩件事：

• 因為脈衝的頻譜全是一，脈衝響應的 DFT 也就等於特徵化系統的濾波器。
• 因此，脈衝響應等於特徵化系統的卷積 window。

10.3 聲音響應 | Acoustic response

想要特徵化房間裡或開闊地的聲音響應，一個簡單的方法是產生一個脈衝，可以是一個氣球爆炸，或是開一槍，這樣會得到一個接近脈衝的輸入訊號，所以你聽到的聲音就接近脈衝響應。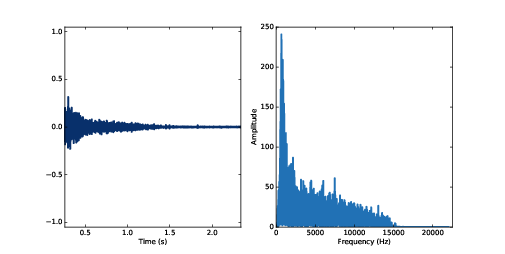

---

圖10.2 槍擊聲的波形

---

現在來個範例，我用一個槍擊聲的錄音來特徵化槍擊發生的房間。然後用脈衝響應模擬該房間的影響作用在小提琴聲音的效果。
範例在 chap10.ipynb，它在這本書的倉儲裡。你可以在後面連結看聽這些範例： http://tinyurl.com/thinkdsp10
槍聲是這樣的：

    response = thinkdsp.read_wave('180961__kleeb__gunshots.wav')
    response = response.segment(start=0.26, duration=5.0)
    response.normalize()
    response.plot()

我從聲音檔的 0.26 秒開始，是為了移掉槍聲開始前的無聲部份。圖10.2 (左)是槍聲的波形，接下來計算響應的 DFT：

    transfer = response.make_spectrum()
    transfer.plot()

結果在圖10.2 (右)。這頻譜把房間的回應編碼了，對於每個頻率，此頻譜皆有一個複數，表示它的振幅增強與相位移。這個頻譜叫做 transfer function，因為它有系統如何將輸入變成輸出的資訊。
現在我們可以模擬這房間的影響作用在小提琴聲音的效果。我們用 1.1節的小提琴錄音：

    violin = thinkdsp.read_wave('92002__jcveliz__violin-origional.wav')
    violin.truncate(len(response))
    violin.normalize()

小提琴與槍聲都是用 44100 Hz採樣，而且剛好持續時間一樣。我把小提琴聲音長度切成與槍聲相同。
接下來就是計算小提琴聲的 DFT：

    spectrum = violin.make_spectrum()

現在我知道輸入的每個頻率成份的振幅與相位，而且也知道系統的 transfer function。它們的乘積就是輸出的 DFT，它可以用來計算輸出的波形：

    output = (spectrum * transfer).make_wave()
    output.normalize()
    output.plot()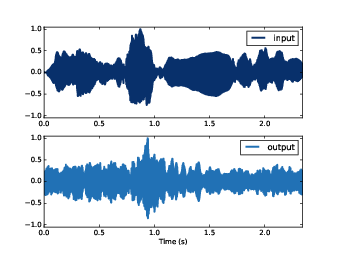

---

圖10.3 在卷積前後的小提琴聲的波形

---

圖10.3 是系統的輸入(上圖)與輸出(下圖)。它們的不同可以被聽出來。載入 chap10.ipynb 然後聽看看。在這例子裡我發現一個驚訝的事，你可以感受這房間的樣子，對我來說，它聽來像是個長形狹窄的房間有著硬地板與天花板，像是個射擊場。
這例子有個沒說的事我先提，免得有人被困擾。小提琴聲實際上已經被一個系統轉換過了，也就是它被錄下的房間。所以例子裡我計算的聲音是被兩個系統轉換過的。為了要更正確模擬在不同房間的小提琴聲音，我應該要特徵化小提琴錄音的房間，然後用它先反特徵化小提琴聲之後再進行模擬。

10.4 系統們與卷積 | Systems and convolution

---

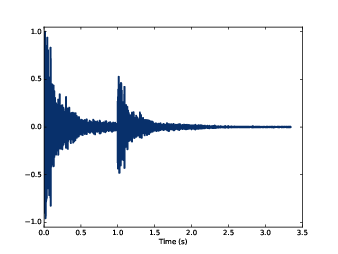
圖10.4 一個波與其位移且縮放過的副本的和

---

如果你認為前節的例子是黑魔法的話，你不是孤單的。我也曾經這麼想過，而且它仍讓我頭痛。
在前節，我建議這樣想像：

• 脈衝是由每個頻率的振幅為 1 的成份們所組成。
• 脈衝響應包含系統對所有成份的響應的和。
• transfer function，其為脈衝響應的 DFT。編碼了系統作用於每個頻率成份，記錄的形式是振幅增強與相位移。
• 對任何輸入，我們可以計算系統的響應，方法是將輸入拆開成各個成份，計算每個成份的響應，再把它加起來。

如果你不喜歡這種方法，有另一個方法可以一起想像：卷積！依據卷積理論，在頻域裡的乘法對應到時域裡的卷積。在這例子裡，系統的輸出是輸入與系統響應的卷積。
這裡有幾個重點可以了解為何這樣可以：

• 你可以想像輸入波的取樣是一系列不同指幅的脈衝。
• 每個輸入的脈衝會得到脈衝響應的副本，有著時間上的位移(因為系統是非時變的)以及縮放過的振幅。
• 輸出會是這些位移、縮放的脈衝響應副本的總和。這些副本可以相加是因為系統為線性的關係。

接下來慢慢看，假設我們不是開一槍，而是開兩槍。第一槍比較大聲在 t=0，振幅為 1。之後比較小聲在 t=1 振幅為 0.5。
我們可以計算系統響應，將原始的脈衝響應與一個縮放移動過的副本加起來。有這個函式可以做出一個波的位移縮放的副本：

def shifted_scaled(wave, shift, factor):
    res = wave.copy()
    res.shift(shift)
    res.scale(factor)
    return res

參數 shift 是時間位移，單位是秒。factor 是乘數因子。
現在來看如何用它來計算兩槍聲的響應：

    shift = 1
    factor = 0.5
    gun2 = response + shifted_scaled(response, shift, factor)

圖10.4 顯示結果。你可以聽到它像 chap10.ipynb 裡的。不意外的你可以聽到像是兩聲槍響，第一聲大於第二聲。
現在，改成不是兩槍，而是 100 槍，每秒開 441 槍。底下迴圈計算結果：

    dt = 1 / 441
    total = 0
    for k in range(100):
        total += shifted_scaled(response, k*dt, 1.0)

因為每秒開了 441 槍，你不會聽到每槍的聲響。你會聽到一個類似週期訊號以 441 Hz 發出的聲音。如果你播放這聲音，它聽起來像車庫裡的汽車喇叭聲。
這為我們帶來一個重要觀點，你可以把任何波都想成一序列的樣本，每個樣本都是一個脈衝有著不同的振幅。
我產生一個 441 Hz 的鋸齒波做一個例子：

    signal = thinkdsp.SawtoothSignal(freq=441)
    wave = signal.make_wave(duration=0.1,
                            framerate=response.framerate)

接下來依序將組成鋸齒波的脈衝巡過一遍，把對應的脈衝響應加總起來：

    total = 0
    for t, y in zip(wave.ts, wave.ys):
        total += shifted_scaled(response, t, y)

這結果聽起來像是在射擊場播放鋸齒波。你仍可以在 chap10.ipynb 聽聽看。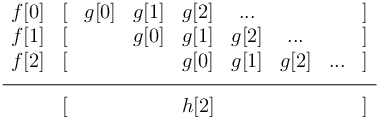

---

圖10.5 g 的縮放平移副本的總和

---

圖10.5 是計算的示意圖，$f$是鋸齒波，$g$是脈衝響應，$h$是 $g$ 的縮放平移副本的總和。
這例子是這樣：
$$h[2]= f[0]g[2]+f[1]g[1]+f[2]g[0]$$
更一般化會是
$$h[n] = \sum_{m=0}^{N-1} {f[m]g[n-m]}$$
你可以認出這方程式來自 8.2節。這是 $f$ 與 $g$ 的卷積。這顯示：如果輸入是 $f$，系統的脈衝響應是 $g$，那輸出是 $f$ 與 $g$ 的卷積。
綜上所述，有兩種方法可以想像系統作用於訊號的影響：

1. 輸入是一序列的脈衝，所以輸出是脈衝響應經位移縮放的總和。那總和就是輸入與脈衝響應的卷積。
2. 脈衝響應的 DFT 是個 transfer function。它將系統對每個頻率成份的作用編碼，形式是記下每個作用的振幅與相位移。輸入的 DFT 則是對其每個頻率成份的振幅與相位移做編碼動作。將輸入的 DFT 乘上 transfer function 會得到輸出的 DFT。

這些描述的相等性不該覺得驚訝，它基本上只是卷積理論的陳述：$f$ 與 $g$ 在時域的卷積對應到在頻域的乘法。
而且之前在談論平滑 window 與 difference window 時，如果你好奇為何卷積要定義成反向，現在你可以知道原因：LTI 系統作用於訊號的響應就自然地出現卷積的定義。

10.5 卷積理論的證明 | Proof of the Convolution Theorem

好吧，我把它放太遠了，現在該是證明卷積理論(Convolution Theorem, CT)的時候，它是這樣說的：
$$DFT(f \ast g)=DFT(f) DFT(g)$$
其中 $f$ 與 $g$ 是相同長度 $N$ 的向量。
我會用兩步前進：

1. 先用一個特例，$f$ 是個複數指數，用 $g$ 卷積，這樣等同於 $f$ 乘上一個純量。
2. 在更通用的例子，當 $f$ 不是個複數指數，我們可以用 DFT 來表示它，也就是複數成份的合，然後計算每個成份的卷積(用乘法)，加總其結果。

結合上面兩步就可以證明卷積理論。但首先，組合我們所需的一些小零件。$g$ 的 DFT，我叫它 $G$：
$$DFT(g)[k] = G[k] = \sum_n {g[n] exp(-2 \pi i n k / N)}$$
其中 $k$ 是頻率的索引，從 0 到 $N-1$；$n$ 是時間的索引，從 0 到 $N-1$。其結果是個向量含有 $N$ 個複數。
$F$ 的 inverse DFT，我叫它 $f$：
$$IDFT(F)[n]=f[n]=\sum_k {F[k] exp(2 \pi i n k / N)}$$
以下是卷積的定義：
$$(f \ast g)[n]=\sum_m {f[m]g[n-m]}$$
$m$ 是另一個時間的索引，從 0 到 $N-1$，卷積符合交換率，所以也可以寫成：
$$(f \ast g)[n]=\sum_m {f[n-m]g[m]}$$
現在，想像一下那個特例，$f$ 是頻率 $k$ 的複數指數，我叫它 $e_k$：
$$f[n]=e_k[n]=exp(2 \pi i n k / N)$$
$k$ 是頻率的索引，$n$ 是時間的索引。
把 $e_k$ 插進第二個卷積的定義而得到：
$$(e_k \ast g)[n] = \sum_m {exp(2 \pi i (n-m) k / N) g[m]}$$
我們可以把第一項拆成一個相乘：
$$(e_k \ast g)[n] = \sum_m {exp(2 \pi i n k / N) exp(-2 \pi i m k / N) g[m]}$$
前半與 $m$ 不相依，所以從 summation 中拉出來：
$$(e_k \ast g)[n] = exp(2 \pi i n k / N) \sum_m {exp(-2 \pi i m k / N) g[m]}$$
現在我們認出第一項是 $e_k$，然後 summation 是 $G[k]$ (用 $m$ 當做時間的索引)。所以我們可以這樣寫：
$$(e_k \ast g)[n] = e_k[n] G[k]$$
這樣顯示，每一個複數指數 $e_k$，與 $g$ 做卷積，有 $e_k$ 乘 $G[k]$ 的效果。用數學話來說，每個 $e_k$ 都是這操作的 eigenvector，$G[k]$ 是對應的 eigenvalue。
接下來是第二部份的證明，如果一個輸入訊號 $f$，不是個複數指數，我們可以藉著計算它的$DFT$(表示成 $F$)而把它表示為複數指數的總和。對於 $k$ 從 0 到 $N-1$ 的每個值，F[k] 都是頻率 $k$ 的成份的複數振幅。
每個輸入成份都是一個複數指數，其振幅為$F[k]$，所以每個輸出成份都是一個複數指數，其振幅是 $F[k] G[k]$，這結論基於第一部份的證明。
因為這個系統是線性的，所以輸出就是輸出成份的總和：
$$(f \ast g)[n] = \sum_k F[k] G[k] e_k[n]$$
把 $e_k$ 插進定義而得到：
$$(f \ast g)[n] = \sum_k F[k] G[k] exp(2 \pi i n k / N)$$
右手邊是 $F$ 與 $G$ 相乘的 inverse DFT，於是：
$$(f \ast g) = IDFT(F G)$$
兩東西要取代，$F=DFG(f)$、$G=DFT(g)$：
$$(f \ast g) = IDFT(DFT(f) DFT(g))$$
最後，兩邊都做 $DFT$，就會得到卷積理論：
$$DFT(f \ast g)=DFT(f) DFT(g)$$
Q.E.D. (證明完畢)

10.6 練習

Solutions to these exercises are in chap10soln.ipynb.
Exercise 1 In Section 10.4 I describe convolution as the sum of shifted, scaled copies of a signal.
But in Section 10.3, when we multiply the DFT of the signal by the transfer function, that operation corresponds to circular convolution, which assumes that the signal is periodic. As a result, you might notice that the output contains an extra note at the beginning, which wraps around from the end.
Fortunately, there is a standard solution to this problem. If you add enough zeros to the end of the signal before computing the DFT, you can avoid the wrap-around effect.
Modify the example in chap10.ipynb and confirm that zero-padding eliminates the extra note at the beginning of the output.
Exercise 2 The Open AIR library provides a “centralized… on-line resource for anyone interested in auralization and acoustical impulse response data” (http://www.openairlib.net). Browse their collection of impulse response data and download one that sounds interesting. Find a short recording that has the same sample rate as the impulse response you downloaded.
Simulate the sound of your recording in the space where the impulse response was measured, computed two ways: by convolving the recording with the impulse response and by computing the filter that corresponds to the impulse response and multiplying by the DFT of the recording.
註：我的線性非時變系統依據： http://en.wikipedia.org/wiki/LTI_system_theory