[超譯]ThinkDSP 第十一章

第十一章 調變與取樣 | Modulation and sampling

在 2.3節我們看到，一個訊號用 10,000 Hz 取樣，在 5500 Hz 的成份會與 4500 Hz 的成份無法分辨。折疊頻率 5000 Hz，是取樣頻率的一半，但我沒有解釋為什麼。
這章探索取樣的效應與展示取樣理論，也會解釋 aliasing 與折疊頻率(folding frequency)。
我會從脈衝卷積的效應開始探索。然後解釋調幅(AM amplitude modulation)，這對於了解取樣理論非常有用。
此章的程式碼在 chap11.ipynb，位置請參閱 0.2節。也可以在後面網址觀看： http://tinyurl.com/thinkdsp-ch11

11.1 用脈衝卷積 | Convolution with impulses

我們之後在 10.4節看過，用一系列的脈衝對一個訊號做卷積，效果為其平移縮放的副本的總和。
來個例子，我現在弄個訊號聽來像個嗶聲的訊號：

filename = '253887__themusicalnomad__positive-beeps.wav'
wave = thinkdsp.read_wave(filename)
wave.normalize()

然後我用四個脈衝建構一個波：

imp_sig = thinkdsp.Impulses([0.005, 0.3, 0.6,  0.9], 
                       amps=[1,     0.5, 0.25, 0.1])
impulses = imp_sig.make_wave(start=0, duration=1.0, 
                             framerate=wave.framerate)

然後對它們做卷積：

convolved = wave.convolve(impulses)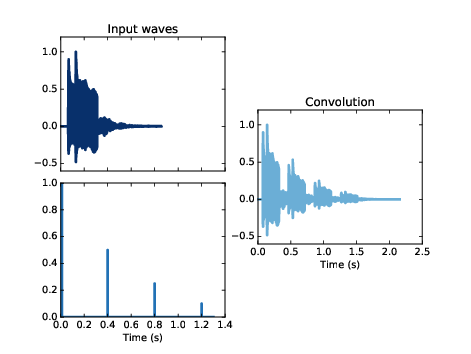

---

圖11.1：(左上圖)訊號與(左下圖)脈衝的卷積效應(右圖)。其效應為原訊號的平移縮放副本的總和。

---

圖11.1 即為其結果。訊號為左上圖，脈衝為左下圖，卷積結果為右圖。
你可以在 chap11.ipynb 聽一下聲音，聽起來像是四個嗶聲，越來越小聲。
這個例子的重點是示範與脈衝做卷積會產生訊號的平移縮放副本的總和。這結論會在下節非常有用。

11.2 調幅 | Amplitude modulation

---

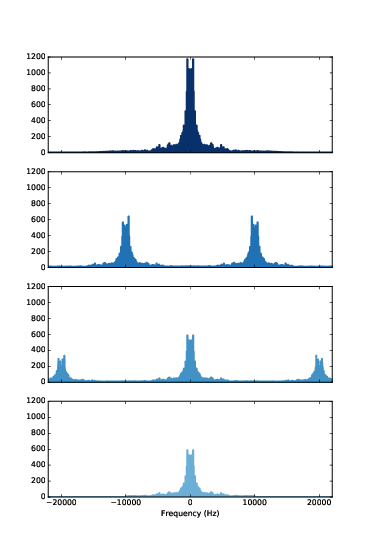
圖11.2：調幅的示範。最上圖是訊號的頻譜。第二圖是調幅後的頻譜。第三圖是去調幅後的頻譜。最下圖是低通過濾後的訊號的去調幅頻譜。

---

AM 調幅用來調幅廣播電波以及其他的應用。在傳輸這端，訊號(可以是說話或音樂等等)被調變，方式是用 cosine 訊號與之相乘，此 cosine 訊號被叫做「carrier wave 載波」。這結果會是個高頻波，而高頻波適合無線電廣播。在美國 AM 電波一般為 500-1600 kHz。( https://en.wikipedia.org/wiki/AM_broadcasting )
在接收端，廣播訊號被「去調幅」以還原成原來的訊號。驚奇地是，去調幅也是把廣播訊號乘上原來的載波就成功。
要看這如何辦到的，我會用個 10 kHz 的載波調變一個訊號。以下是訊號：

filename = '105977__wcfl10__favorite-station.wav'
wave = thinkdsp.read_wave(filename)
wave.unbias()
wave.normalize()

然後是載波：

carrier_sig = thinkdsp.CosSignal(freq=10000)
carrier_wave = carrier_sig.make_wave(duration=wave.duration, 
                                     framerate=wave.framerate)

我們用 $\ast$ 這個操作元，將它們相乘，這是 wave array 元素的操作：

modulated = wave * carrier_wave

這結果聽起來非常糟，你可以在 chap11.ipynb 聽聽看。
圖11.2 顯示了在頻域發生什麼事。最上是原來訊號的頻譜。接著是乘上載波成為調變過的訊號，由兩個原頻譜平移正負 10 kHz的成份組成。
要了解為什麼，要回憶一下，在時域的卷積對應在頻域的乘法。反過來說，時域中的乘法對應到頻域中的卷積。當我們把訊號乘上載波，就等於用載波的 DFT 與訊號的頻譜做卷積。
因為載波是簡單 cosine wave，它的 DFT 為兩個脈衝，在正負 10 kHz。用這些脈衝做卷積，得到平移縮放的副本的頻譜。注意看，在調變之後的頻譜的振幅變小。其能量從原訊號被分成兩個副本。
我們去調變這訊號，就是再乘上載波一次：

demodulated = modulated * carrier_wave

圖11.2 的第三圖就是它的結果。再一次看到，時域中的乘法對應頻域中的卷積，它產生平移縮放過的調譜副本總和。
因為調變過的頻譜有兩個尖起，每個尖起高度僅有一半，並分成兩半，平移正負 20 kHz，兩個副本在 0 kHz 碰在一起又加起來。另外兩半距中心正負 20 kHz。
如果你聽去調變的訊號，它聽來很棒。頻譜副本有額外多出高頻成份，但因為頻率太高，一般喇叭放不出來，多數人也聽不出來。如果你有好音響也有好耳朵，就可能聽得到。
你可以用低通濾波去掉那些額外的成份：

demodulated_spectrum = demodulated.make_spectrum(full=True)
demodulated_spectrum.low_pass(10000)
filtered = demodulated_spectrum.make_wave()

這結果非常接近原來的波，雖然經過去調變與濾波後失去約一半的能量。在實務上這不是太大問題，因為有更多的能量在傳送與接收廣播訊號的過程中損失。反正我們都必須要增強振幅，那個 2 的因數就不會是個問題。

11.3 取樣 | Sampling

---

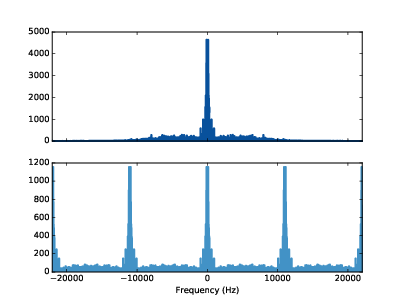
圖11.3：取樣前後的訊號頻譜

---

我用調幅解釋，部份原因是因為它有趣，但更多的是它可以幫助我們了解「sampling 取樣」。取樣是在時間上依序量測類比訊號的程序，通常是用相同時間間隔。
例如，我們先前使用的 WAV 檔就是使用類比轉數位的轉換器(analog-to-digital converter ADC)採集麥克風的輸出。取樣率大多是 44.1 kHz，這是 CD 品質的聲音的標準速率，或是 48 kHz，這是 DVD 聲音的標準。
在 48 kHz 的情況下，折疊頻率是 24 kHz，這稍微高於多數人可聽到的頻率。( https://en.wikipedia.org/wiki/Hearing_range )
這些波的多數是用 16 bits 記錄，所以是 $2^16$ 個階級。這個「bit depth 位元深度」已經足夠，再多增加深度也沒有增加多少音質( https://en.wikipedia.org/wiki/Digital_audio )
當然，聲音之外的應用會需要更高的取樣率以採取更高的頻率，或更深的位元深度以獲得更高還原度的波形。
要示範取樣的效應，我一開始用 44.1 kHz 取樣率的波，然後用 11 kHz 取樣率取樣。這並不完全等同於直接從類比訊號取樣，但效應相同。
首先，載入一段鼓的獨奏：

filename = '263868__kevcio__amen-break-a-160-bpm.wav'
wave = thinkdsp.read_wave(filename)
wave.normalize()

圖11.3 上圖是波的頻譜。再來是從波的取樣的函數：

def sample(wave, factor=4):
    ys = np.zeros(len(wave))
    ys[::factor] = wave.ys[::factor]
    return thinkdsp.Wave(ys, framerate=wave.framerate)

我用這個每四個元素挑出一個當樣本：

sampled = sample(wave, 4)

其結果與原始訊號有相同的 frame rate，但大多元素為零。如果你播放這個波，聽來不是很好。這個取樣程序引入原來不存在的高頻成份。
圖11.3 下圖是取樣過的頻譜，它包含了四個原始頻譜的副本(它看來有五個副本，因為其中一個被分兩半於最高與最低頻)。

---

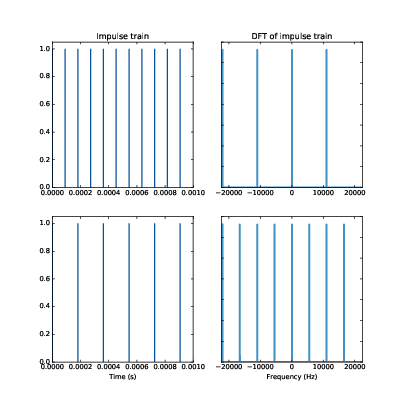
圖11.4：脈衝火車的 DFT 也是個脈衝火車

---

要了解這些副本從何而來，我們可以想像取樣程序為乘上一系列的脈衝。不用 sample 每四個元素選一個，我們改用以下函數產生一系列的脈衝，有時會叫它脈衝火車。

def make_impulses(wave, factor):
    ys = np.zeros(len(wave))
    ys[::factor] = 1
    ts = np.arange(len(wave)) / wave.framerate
    return thinkdsp.Wave(ys, ts, wave.framerate)

接著原來波乘上脈衝火車：

impulses = make_impulses(wave, 4)
sampled = wave * impulses

結果一樣，它聽來不是很好，但現在我們了解原因。在時域的乘法對應頻域的卷積。當我們乘上脈衝火車，我們等於與脈衝火車的 DFT 做卷積。結論，脈衝火車的 DFT 也是個脈衝火車。
圖11.4 展示兩個例子，上面一列是例子中的脈衝火車，頻率 11025 Hz。其 DFT 是 4 個脈衝的火車，這就是為何我們得到 4 個頻譜的副本。下面一列展示一個脈衝火車，頻率較低，約 5512 Hz。它的 DFT 是 8 個脈衝的火車。一般來說，在時域中越多脈衝在時域就對應越少脈衝。
總結：

• 我們可以想像取樣是乘上脈衝火車
• 乘上脈衝火車對應於頻域與脈衝火車卷積
• 與脈衝火車卷積產生數個訊號頻譜

11.4 混疊 | Aliasing

---

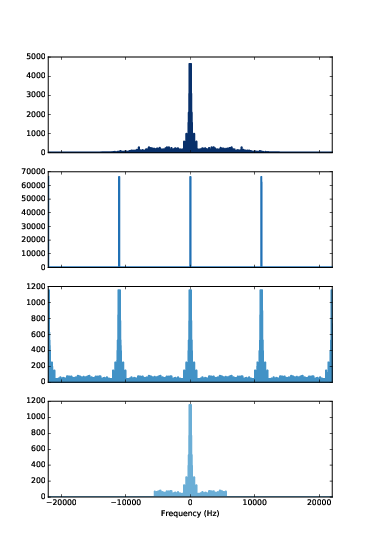
圖11.5：最上圖，鼓獨奏的頻譜。第二圖，脈衝火車的頻譜。第三圖，取樣過的波的頻譜。最下圖，取樣波經過低通濾波後的頻譜。

---

11.2節，在示範過調幅之後，我們用低通濾波把多餘的副本去掉。我們也可以在取樣之後做一樣的事，但它顯然不是個完美的解法。
圖11.5 說明為何不是。最上圖是鼓獨奏的頻譜。它包含超過 10 kHz 的高頻成份。當我們對這波取樣，我們用脈衝火車(第二圖)對其卷積，會產生一些頻譜副本(第三圖)，最下圖是應用低通濾波後的結果，切在折疊頻率 5512 Hz。
如果我們將結果轉回波，它是近似於原來的波，但有兩個問題：

• 因為低通濾波器，超過 5500 Hz的成份會遺失，那些聲音被消音。
• 低於 5500 Hz 的成份也不完全對，因為它們混有其他副本的聲音，而我們沒法濾掉。

---

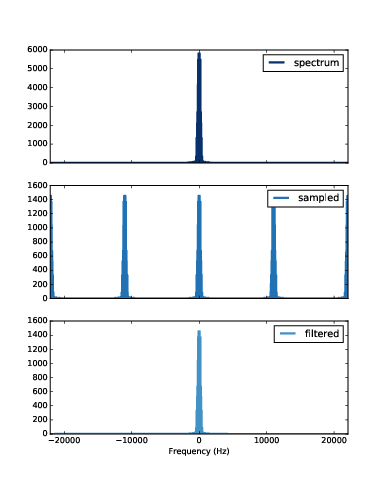
圖11.6：低音吉他的頻譜(上圖)，取樣後的頻譜(中)，濾過後的頻譜(下)

---

如果在取樣後的頻譜副本有重疊，我們就會失去頻譜內的資訊，而且無法還原它。
但如果頻譜副本沒有重疊，這方法就會很棒。第二個例子，我們載入低音吉他獨奏的聲音。
圖11.6 上圖為它的頻譜，在 5512 Hz 以上無可見能量。第二圖是取樣波的頻譜。第三圖是低通濾波後的頻譜。振幅稍微小一點因為我們濾掉一些能量，但頻譜的形狀與原始的幾乎完全一樣。如果我們轉回波，它聽來一樣。

11.5 插值 | Interpolation

---

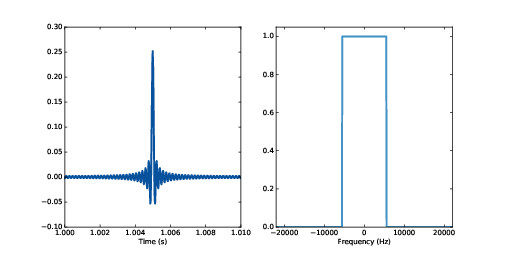
圖11.7：磚牆低通濾波器(右)與對應的卷積 window

---

上一步我用的低通濾波器俗稱磚牆濾波器，超過切線的頻率全部切乾淨，就好像撞到磚牆一樣。
圖11.7 (右)就是濾波器的長相。當然，在頻域乘上這濾波器就對應於時域與其卷積。我們可以知道這 window 是計算濾波器的 inverse DFT，它長相在圖11.7 左圖。
這函數有個名字，叫做 normalized sinc function。它有個離散逼近的版本( https://en.wikipedia.org/wiki/Sinc_function )：
$$sinc(x) = \frac {sin \pi x} {\pi x}$$
當我們想用低通濾波器，就等同使用 sinc 函數做卷積。我們可以想像此卷積為平移縮放過的 sinc 函數副本的總和。
sinc 的值在 x=0 為 1，在 x 其他整數值為 0。要平移 sinc 函數時，我們是移動零點。要縮放它時，我們改變零點的高度。所以當我們要加總平移縮放的副本時，需要在取樣點中間插值。

---

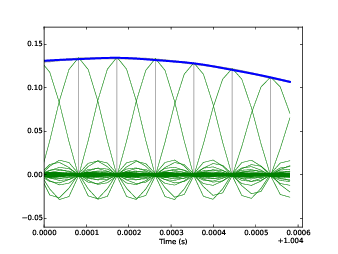
圖11.8：近看取樣點(直灰線)、插值 sinc 函數(細曲線)、原始波(上方的粗線)

---

圖11.8，用低音吉他的聲音段來看這是什麼回事。上方橫跨的粗線是原始的波。直灰線是取樣的值。細線是平移縮放的 sinc 函數副本。這些 sinc 函數總和就等同原始波。
重要的事值得再說一次：

這些 sinc 函數總和就等同原始波。

因為我們一開始的訊號在 5512 Hz 左右沒有能量，我們用 11025 Hz 取樣，我們可以完全還原原始頻譜。而如果我們有原始頻譜，我們就可以還原原始波。
在這個例子，我們的波已經用 44100 Hz 取樣，然後我再用 11025 Hz 取樣。再次取樣後，頻譜副本的間隙是 11025 Hz。 (譯註：原文 11025 kHz 應該是 typo)
如果原波在 5512 Hz 以上沒有能量，頻譜副本沒有重疊，我們不會搞丟其中資訊，就可以完全還原原始訊號。
這結論就是著名的「Nyquist-Shannon sampling theorem 奈奎斯特 取樣理論」 ( 參閱 https://en.wikipedia.org/wiki/Nyquist-Shannon_sampling_theorem )
這例子沒有證明取樣理論，但我希望它幫你了解取樣理論在說什麼以及怎麼辦到的。
注意我說的並沒有依據原始的取樣率 44.1 kHz。如果我採用更高的取樣率，結論還是會一樣。甚至原訊號為類比連續也一樣。如果我們取樣率為 $f$，要能完全還原原訊號，只要在 $f/2$ 的地方沒有能量即可。這樣的訊號會叫它 bandwidth limited。

11.6 總結 | Summary

恭喜，你到了本書最後(好吧，還有一些練習在後面)(譯註：我也鬆一口氣)。在你離開前，我來回顧一路走來的重點：

• 我們從週期訊號與其頻譜開始，並引入 thinkdsp 函式庫中重要的物件：Signal、Wave、Spectrum。
• 我們檢視簡單波形與樂器錄音的諧波結構，並且看見混疊(aliasing)的效應。
• 使用光譜圖(spectrogram)，我們探索唧聲與其他會隨時間改變頻譜的聲音。
• 我們產生並分析噪音訊號，並特徵化噪音的自然來源。
• 我們使用自相關函數估算音高與噪音的附加特徵。
• 我們學會「離散餘弦轉換 Discrete Cosine Transform (DCT)」，它對壓縮非常有用，也進一步了解「離散傅立葉轉換 Discrete Fourier Transform (DFT)」。
• 我們使用複數指數合成複數訊號，然後反轉這過程來發展 DFT。如果你有做該章最後的練習，你會實作快速傅立葉轉換，這是 20 世紀最重要的演算法。
• 從平滑化開始，展示卷積的定義，描述卷積理論，它將時域中平滑化的操作與頻域中濾波器的操作關聯起來。
• 我們探索微分與積分當成線性濾波器，它是解微分方程組的方法的基礎。它也解釋一些之前章節見過的效應，像是白噪音與布朗噪音的關聯。
• 我們學會線性非時變(LTI)系統的理論，以及使用卷積理論，以他們的脈衝響應特徵化 LTI 系統。
• 我展示「調幅 amplitude modulation (AM)」，它在廣播通訊上非常重要，也進一步了解取樣理論，它有令人驚訝的結論，對於數位訊號處理非常重要。

如果你已經到了這裡，你應該對於實作上，如何使用工具處理訊號，與理論上，了解取樣與濾波器的工作原理，有著非常平衡的理解。
我希望你在過程中獲得快樂，謝謝！

11.7 練習

Solutions to these exercises are in chap11soln.ipynb.
Exercise 1 The code in this chapter is in chap11.ipynb. Read through it and listen to the examples.
Exercise 2 Chris “Monty” Montgomery has an excellent video called “D/A and A/D | Digital Show and Tell”; it demonstrates the Sampling Theorem in action, and presents lots of other excellent information about sampling. Watch it at https://www.youtube.com/watch?v=cIQ9IXSUzuM .
Exercise 3 As we have seen, if you sample a signal at too low a frame rate, frequencies above the folding frequency get aliased. Once that happens, it is no longer possible to filter out these components, because they are indistinguishable from lower frequencies.
It is a good idea to filter out these frequencies before sampling; a low-pass filter used for this purpose is called an anti-aliasing filter.
Returning to the drum solo example, apply a low-pass filter before sampling, then apply the low-pass filter again to remove the spectral copies introduced by sampling. The result should be identical to the filtered signal.